И дело тут не только в огромной скорости снарядов.
Для самого примитивного понимания, давайте возьмем бочку в форме куба. И пусть сторона этого куба будет равняться одному метру.
Каким будет объем этого куба? Правильно – 1 кубический метр (1*1*1=1).
Теперь увеличим каждую сторону в 2 раза, чтобы куб получился 2 на 2 на 2 метра.
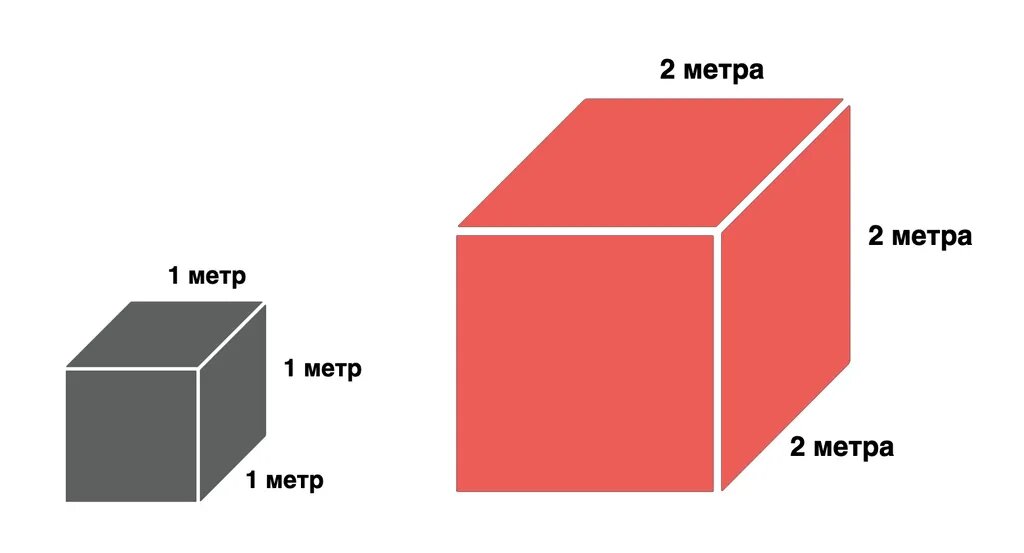
Во сколько раз увеличится объем этого куба? Он увеличится вовсе не в 2 раза, а намного больше – это видно даже по картинке.
Если посчитать, то объем нового куба это 2*2*2=8 кубических метров, что в 8 раз больше, чем у первоначального куба.
Увеличив сторону в 3 раза, мы увеличим объем в 27 раз (3*3*3=27). А если увеличить сторону в 10 раз, то объем вырастет вообще в 1000 раз (10*10*10=1000).
Таким образом, 3-мерные объекты (куб, шар, цилиндр, пирамида и т.д.) находятся в зависимости от своих линейных размеров, но только не напрямую, а как бы в «кубической» зависимости.
Вот даже взять формулу объема шара. И там тоже будет эта хитрая цифра 3 (возведение в третью степень):
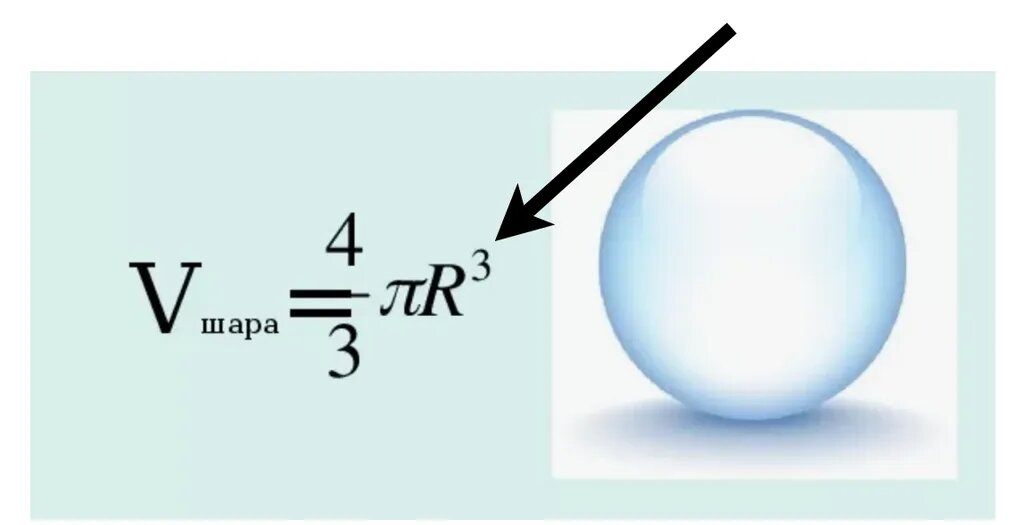
То есть для шара справедливо всё то же самое, что и для куба: увеличиваем радиус в 3 раза, а объем увеличивается сразу в 27 раз.
Теперь смотрите, что такое любой взрыв? По форме это примерно и есть – шар. То есть разлетающаяся во все стороны «облако».

Ну, если бы взрыв происходил в космосе, то там он может и правда представлял из себя идеальный шар. Но на Земле этот шар встречает много препятствий. Например, поверхность этой самой Земли.

Шар бьётся о поверхность и выбивает в ней углубление – воронку.

Кстати, то что воронка всегда круглая (даже если снаряд упал под углом) наглядно демонстрирует «шарообразность» взрыва.
Посмотрите на Луну – она вся в воронках (кратерах). И все они круглые, нет ни одной вытянутой в овал.

Это при том, что метеориты на Луну падают под самыми разными углами. Далеко не все падают вертикально. Но воронка всегда идеально круглая, просто потому что в момент удара возникает взрыв и этот взрыв – всегда шарообразный.
С этим понятно. Теперь следующий вопрос:
А от чего зависит диаметр этой самой воронки?
Логично предположить, что от количества высвобождаемой энергии.
Чем больше энергии у взрыва >> тем больше диаметр взрывного шара >> тем больший диаметр воронки остается.
Меньше энергии – меньше шар – меньше воронка. И наоборот.
И вот тут давайте вернемся к тому, с чего мы начали. Зависимость объема шара от его линейных размеров – «кубическая».
Чтобы увеличить объем шара в 27 раз достаточно увеличить его радиус всего в 3 раза. Звучит вроде неплохо, но ведь это же правило работает и в обратную сторону: если мы увеличим объем шара в 27 раз, то радиус шара увеличится всего лишь в 3 раза.
Вот тут-то собака и зарыта.
Если некий снаряд оставляет воронку радиусом 1 метр, то для того, чтобы получить воронку радиусом 2 метра (всего в 2 раза больше), нужно не в 2 раза более мощный взрыв, а в 8 раз более мощный (2*2*2=8).
Представляете?
Чтобы получить воронку радиусом в 10 метров, нужен взрыв в 1000 раз более мощный!
Этот физический закон является большим ограничением для оружейников. Собственно, с какого-то момента просто теряется особый смысл увеличивать мощность взрыва, т.к. взрывчатки ты можешь положить в 1000 раз больше, а эффект получится бОльшим лишь в 10 раз.
Конечно, это всё утрировано и крайне примитивно описано, но, думаю, так будет понятнее большинству.
- Например, обычный артиллерийский боеприпас оставляет в земле воронку диаметром 1,5 метра. При этом взрывчатки в нем всего килограммов 10.
- А ядерная бомба мощностью 700 килотонн (т.е. 700 миллионов килограмм взрывчатки) оставляет воронку диаметром 300 метров. Чувствуете соотношение? Мощность бомбы в 70 миллионов раз больше, чем у снаряда, а воронка получается больше всего в 200 раз.

Как же обойти это ограничение?
Главный способ – дробить один большой заряд на много маленьких.
Допустим, у нас есть 8 тонн взрывчатки. Мы можем:
- А) Взорвать все эти 8 тонн в одной точке
- Б) Разделить 8 тонн на 8 частей (по 1 тонне) и взорвать их в разных местах
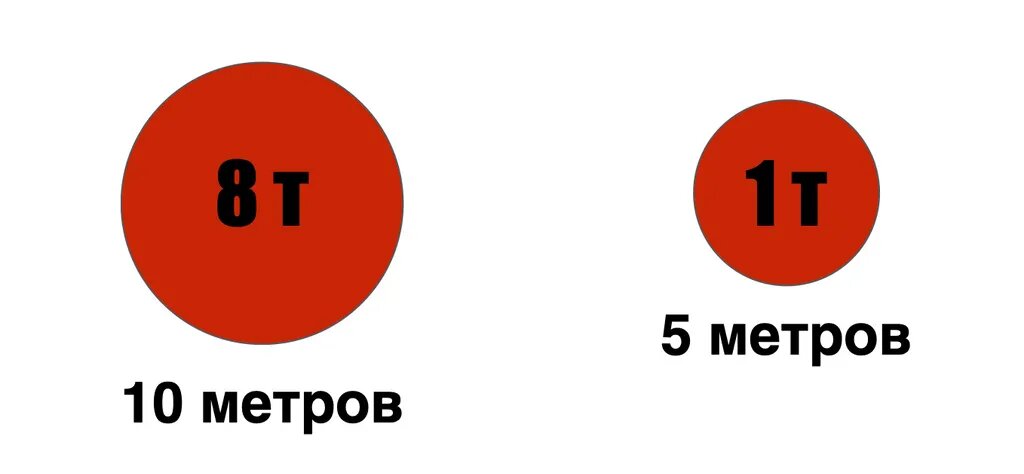
Да, при взрыве 8-тонного заряда образуется более крупная воронка, чем при взрыве 1-тонного заряда. Но разница в размерах там не в 8 раз, а всего в 2 раза (2*2*2=8).
То есть, если 8-тонный снаряд оставляет, например, 10-метровую воронку, то 1-тонный – 5 метровую.
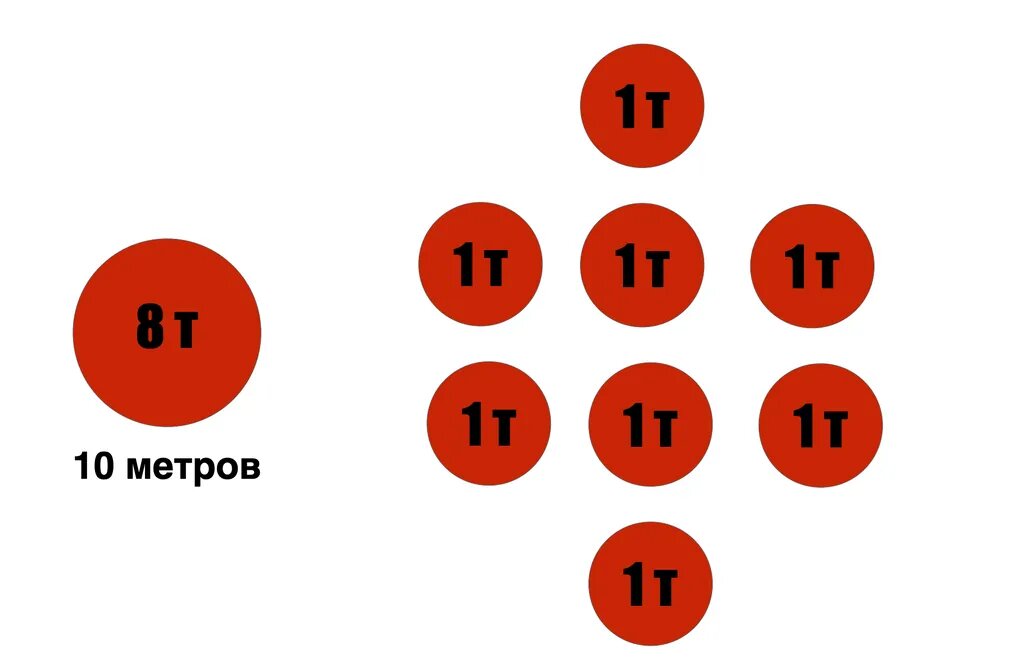
Но зато таких 5-метровых воронок у нас будет аж 8 штук! И мы можем разложить их в разных точках так, что общий эффект получится намного более разрушительным, чем от взрыва всех 8 тонн в одной точке:
ВАЖНО! Под воронками, конечно же, мы понимаем не только сами воронки, но и все разрушения, которые приносит взрыв (вплоть до выбитых окон и контузий людей). Просто все эти разрушения и повреждения точно так же распространяются от точки взрыва «кольцеобразно» во все стороны.
Думаю, теперь вы понимаете, в чем фишка «Орешника», который делится даже не на 8, а на 36 частей (6 боеголовок по 6 суббоеприпасов в каждом)!
В прошлой статье мы посчитали, что даже в кинетическом исполнении (без начинки, просто как болванка) весь «Орешник» целиком несет такую же энергию, как 6 тонн тротила (за счет огромной энергии движения).
Если добавить в боеголовки взрывчатку – получится эквивалент около 10 тоннтротила. Но! Эти 10 тонн будет разделены на 36 частей. Грубо говоря, по 300 кг тротилового эквивалента в каждой.
Теперь представим, что эти 36 частей падают с промежутками в 100 метров друг от друга. Вполне достаточно, чтобы все, что осталось внутри этих 100 метров – погибло и разрушилось.
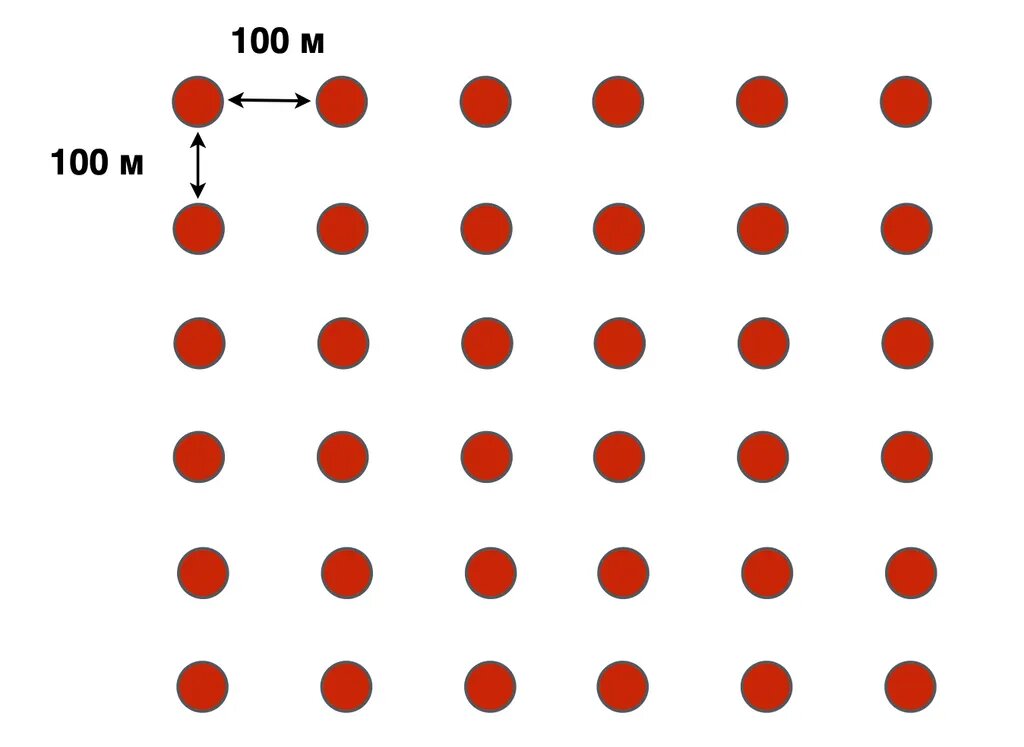
Общий размер этого квадрата – 600 на 600 метров.
То есть 600 на 600 метров сплошных разрушений. Подобного эффекта можно добиться только тактическим ядерным оружием. Скажем, 20 килотонн, взорванных в одной точке будут нести примерно те же разрушения.
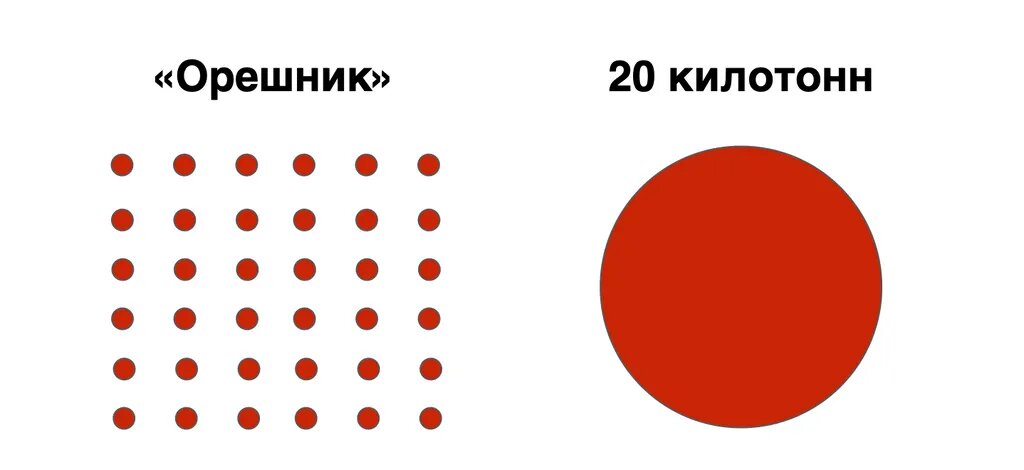
Но только то будет ядерный взрыв, со всеми вытекающими (от радиации до политических последствий). А «Орешник» – это безъядерный боеприпас.
Хотя… Если его еще и ядеркой снабдить… Даже по 20 килотонн на боеголовку… Представляете, 36 снарядов по 20 килотонн в каждом? Разрушительный эффект будет как от «Царь-бомбы», если не больше.
